4.1.9 桶排序
思想:桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的N个数据均匀的分配到K个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
什么时候最快(Best Cases):
当输入的数据可以均匀的分配到每一个桶中
什么时候最慢(Worst Cases):
当输入的数据被分配到了同一个桶中 |
设置固定空桶数
将数据放到对应的空桶中
将每个不为空的桶进行排序
拼接不为空的桶中的数据,得到结果
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; //输入数据的最小值
} else if (arr[i] > maxValue) {
maxValue = arr[i]; //输入数据的最大值
}
}
//桶的初始化
var DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
//利用映射函数将数据分配到各个桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); //对每个桶进行排序,这里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
维基百科: JavaScript实现算法
分类 排序算法
数据结构 数组
最坏时间复杂度 O(n^{2})
平均时间复杂度 O(n+k)
最坏空间复杂度 O(n*k)
桶排序以下列程序进行:
设置一个定量的数组当作空桶子。
寻访序列,并且把项目一个一个放到对应的桶子去。
对每个不是空的桶子进行排序。
从不是空的桶子里把项目再放回原来的序列中。
Array.prototype.bucketSort = function(num) {
function swap(arr, i, j) {
const temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
const max = Math.max(...this)
const min = Math.min(...this)
const buckets = []
const bucketsSize = Math.floor((max - min) / num) + 1
for(let i = 0; i < this.length; i++) {
const index = ~~(this[i] / bucketsSize)
!buckets[index] && (buckets[index] = [])
buckets[index].push(this[i])
let l = buckets[index].length
while(l > 0) {
buckets[index][l] < buckets[index][l - 1] && swap(buckets[index], l, l - 1)
l--
}
}
let wrapBuckets = []
for(let i = 0; i < buckets.length; i++) {
buckets[i] && (wrapBuckets = wrapBuckets.concat(buckets[i]))
}
return wrapBuckets
}
const arr = [11, 9, 6, 8, 1, 3, 5, 1, 1, 0, 100]
console.log(arr.bucketSort(10))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
操作步骤说明:
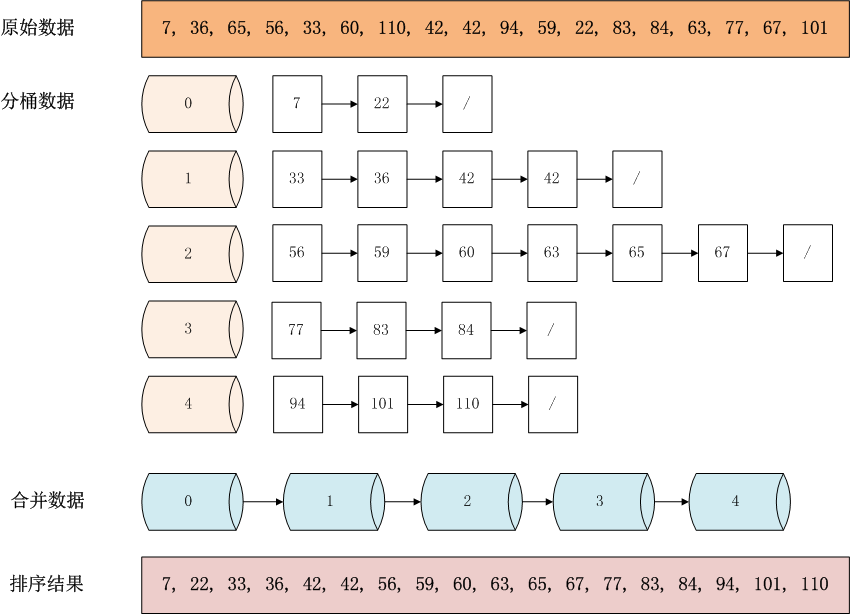
- 设置桶的数量为5个空桶,找到最大值110,最小值7,每个桶的范围20.8=(110-7+1)/5 。
- 遍历原始数据,以链表结构,放到对应的桶中。数字7,桶索引值为0,计算公式为floor((7 – 7) / 20.8), 数字36,桶索引值为1,计算公式floor((36 – 7) / 20.8)。
- 当向同一个索引的桶,第二次插入数据时,判断桶中已存在的数字与新插入数字的大小,按照左到右,从小到大的顺序插入。如:索引为2的桶,在插入63时,桶中已存在4个数字56,59,60,65,则数字63,插入到65的左边。
- 合并非空的桶,按从左到右的顺序合并0,1,2,3,4桶。
- 得到桶排序的结构